
Puzzle Monday: Going Home
Editor’s Note, November 2024: Thanks for checking out our puzzle archive! While the online version of this puzzle is no longer interactive, we suggest downloading the PDF, available below. You can find other archived puzzle PDFs available for download here.
Among our crosswords and other puzzles, we’ll be featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.
There is a lot of competition in the pages of Puzzle Communication Nikoli, the world’s most influential puzzle publication. Most of the puzzles in the publication are contributed by users—and they contribute a lot of ideas. Some concepts catch on, with other readers handcrafting new examples for publication, and eventually earning a regular place in its pages, while others might not make the cut. These puzzles might evolve into others or fade from memory. But occasionally an idea can come home.

Satogaeri, which translates to “Homecoming,” was created by the Nikoli reader with the pseudonym Ichinokoto in 2002. It was the evolution of a puzzle called Bonsan that the reader had created before, involving numbers, arrows, and symmetry. He evolved aspects of it into Satogaeri. According to to Nikoli president and puzzle editor Yoshinao Anpuku, both puzzles were well-received on release, but seemed to split popularity. Satogaeri was soon retired. Nikoli, it turns out, is a tough place to stick.
But all was not lost. In 2013, Nikoli launched a subscription-based puzzle site online, and Satogaeri found a second life. This time, it stuck. And though the puzzle site is now itself retired, Satogaeri earned enough fans to make it back home, to the pages of the print magazine.
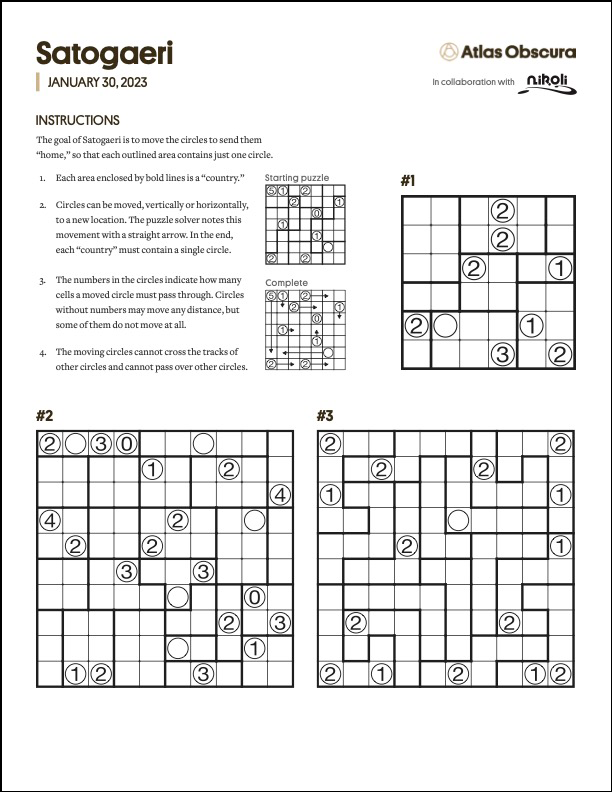
Fittingly, the puzzle is inspired by global migration and the sense of home. The goal is to move the circles to send them “home,” so that each outlined area contains just one circle.

- Each area enclosed by bold lines is a “country.”
- Circles can be moved, vertically or horizontally, to a new location. The puzzle solver notes this movement with a straight arrow. In the end, each “country” must contain a single circle.
- The numbers in the circles indicate how many cells a moved circle must pass through. Circles without numbers may move any distance, but some of them do not move at all.
- The moving circles cannot cross the tracks of other circles and cannot pass over other circles.
Stumped? Download the solutions!









Follow us on Twitter to get the latest on the world's hidden wonders.
Like us on Facebook to get the latest on the world's hidden wonders.
Follow us on Twitter Like us on Facebook